Rotating Towers

What You’ll Learn

In this section, we will break down the process of rotating towers so that they always face a balloon.

Key Concepts

1. Understanding slope of a line and how it can help determine direction
2. Using the components of slope to come up with an angle of rotation
3. Using the angle of rotation to rotate the tower

Remember that in Processing, Y values increase as you move down the window. Therefore, the origin (0,0) is at the top-left corner of the window.

The Connection Between the Slope of a Line and Direction

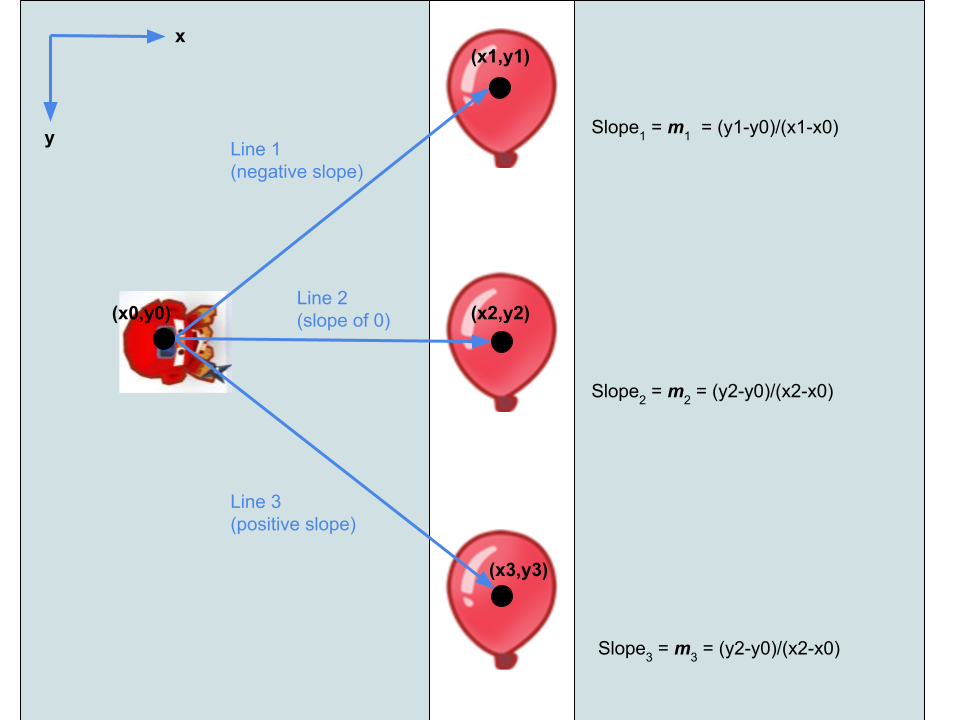
The slope of a line is essentially a measure of incline. This incline is determined by how the hieght of the line changes as you move along the X-axis. Take a look at line 1. As you move along the x-axis (go from left to right), the height (or Y-value) of the line decreases, and so we say it has a negative incline, or slope value. In line 2, the line’s height doesn’t change, so we say it has a slope of 0 (no incline). For line 3, the height/Y-value increases as you move along the X-axis, so we say the slope is positive. As you may see, the slope of a line contains some information about the direction from one point to another.

To mathematically find slope of a line connection 2 points, you must take 2 points on the line: (x1,y1) and (x2,y2). The you must calculate the change in Y, which we call rise, and the change in X, which we call run. Change in Y is equal to y2-y1, and change in X is equal to x2-x1. We can then divide rise by run, which is the same thing as (y2-y1)/(x2-x1).

Slope -> Angle

Now we can use the components of slope (rise and run), to calculate the angle at which the tower must turn. To do this, we will use atan2(), and use rise as our first input, and run as our second input.

float angle = atan2(balloonY-towerY,balloonX-towerX);

Rotating the Tower

Now we can use pushMatrix() and popMatrix(). These functions are used if you want to apply transformations to just one or a group of shapes, and not the whole screen. In this case, we translate() the origin to the tower’s coordinates (since all things rotate relative to the origin), and we’ll rotate() the tower so that it faces the balloon.

void drawTower(){
  float angle = atan2(balloonY-towerY,balloonX-towerX);

  line(towerX,towerY,balloonX,balloonY);

  pushMatrix();

  translate(towerX,towerY);

  rotate(angle);

  triangle(20,0,-20,-20,-20,20);

  popMatrix();
}

And there you go! Now you know how to rotate a tower so that it faces a balloon!